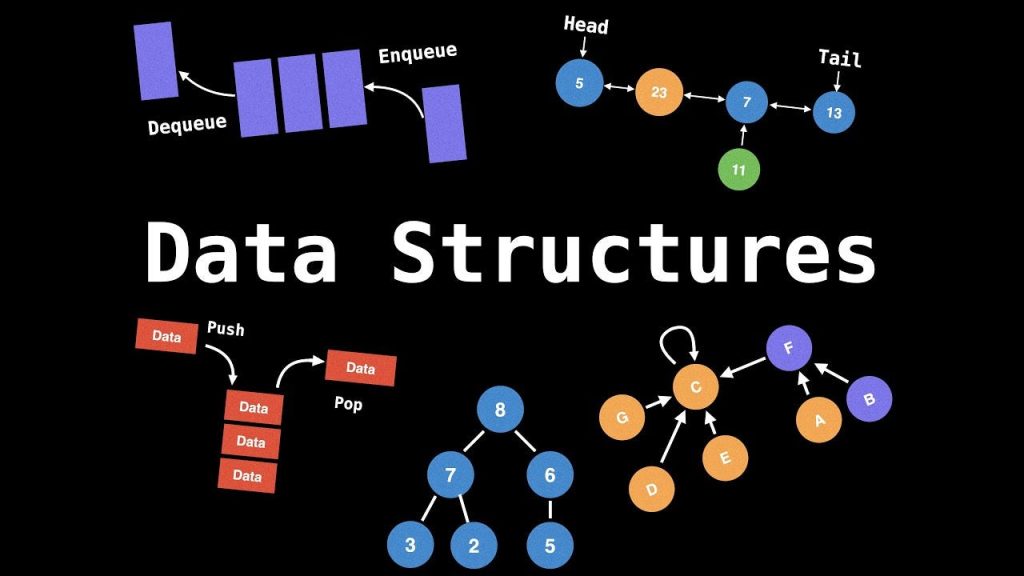
In the world of programming, data structures and algorithms are like the backbone and the brain of software.
- Data structures help you organize and store data in a systematic way.
- Algorithms help you process data quickly and accurately.
A good programmer not only knows how to write code that works, but also knows how to optimize time and memory by choosing the appropriate data structures and algorithms. In this article, we will explore data structures and algorithms—from basic concepts and common types to how they work together to create programs that are both fast and resource-efficient.

1. What Is a Data Structure?
1.1. Definition
A data structure is a way of arranging, organizing, and storing data in a computer so that it can be accessed and processed efficiently.
In a more illustrative way if data is a pile of books, documents, and files, then a data structure is the way you arrange them on shelves, classify them by topic, label them, or put them into boxes so that you can find them again as quickly as possible later.
In computer science, “efficiency” here is measured by:
- Time: How long does it take to search, insert, delete, or update data? (measured using Big-O complexity: O(1), O(log n), O(n), …)
- Memory: How much space is required to store the data? Is there any waste?
- Flexibility: How easy is it to extend or modify when the problem requirements change?
Key point: The same data, when organized in different ways, can make a program run fast enough for you to leave work on time—or slow like waiting for your crush to reply to your messages.
Example: finding someone’s phone number
- If you store phone numbers in a long sheet of paper with 10,000 lines and read from top to bottom → it takes O(n) time.
- If you store them in a sorted contact list and use binary search → it takes only O(log n) time.
- If you store them in a hash table → on average, it takes O(1) time to find it immediately.
1.2. Common Characteristics of Data Structures
Organizing and storing data: Each data structure defines how data is arranged in memory (contiguously or non-contiguously).
Examples:
- Arrays → stored contiguously.
- Linked lists → stored non-contiguously, connected by pointers.
Data access and operations: Each type of data structure supports basic operations such as:
- Insert
- Delete
- Search
- Traverse
Depending on the structure, the execution speed differs (O(1), O(log n), O(n), …).
Relationships between elements: Elements have logical relationships (order, hierarchy, parent–child relationships, etc.).
Examples:
- Stack → LIFO relationship.
- Queue → FIFO relationship.
- Tree → hierarchical relationship.
Abstraction: Data structures are often defined by their operations rather than their specific implementations (Abstract Data Type – ADT).
Example: A “stack” only requires operations such as push and pop; whether it is implemented using an array or a linked list is optional.
Time and memory efficiency: Each data structure has its own advantages and disadvantages in terms of:
- Memory usage.
- Operation execution time.
Choosing the appropriate data structure directly affects the performance of a program.
1.3. The Role of Data Structures
Data structures play a foundational role in programming and computer science, specifically
Optimizing program performance: Choosing the right data structure can reduce execution time from hours to just seconds.
Saving memory: Proper organization helps minimize wasted space, especially with large datasets.
Ease of maintenance and scalability: Source code becomes cleaner and clearer when data is managed systematically.
Solving complex problems: Advanced algorithms (such as shortest path finding, scheduling, and data analysis) rely heavily on appropriate data structures.
Foundation for learning algorithms: Many algorithms are only effective when paired with the correct type of data structure (for example, Dijkstra’s algorithm requires a priority queue).
1.4. Common Types of Data Structures
Linear Data Structures
| Type | Description |
|---|---|
| Array | Stores elements contiguously in memory. Provides fast access but has a fixed size. |
| Linked List | Elements are connected through pointers. Flexible in size. |
| Stack | LIFO (Last In, First Out) structure. |
| Queue | FIFO (First In, First Out) structure. |
Non-linear Data Structures
| Type | Description |
|---|---|
| Tree | Each node can have multiple child nodes. Used to represent hierarchical structures. |
| Graph | Consists of vertices and edges, representing relationships between objects. |
Abstract Data Types (ADT)
| Type | Description |
|---|---|
| List | An ordered collection of elements. |
| Set | A collection with no duplicate elements. |
| Hash Table | Stores data as key–value pairs. Provides fast access. |
| Priority Queue | A queue in which elements with higher priority are processed first. |
Special Data Structures
| Type | Description |
|---|---|
| Heap | A special binary tree used to quickly find the maximum or minimum value. |
| Trie (Prefix Tree) | A tree used to store strings, especially for dictionaries. |
| Segment Tree / Fenwick Tree | Advanced structures used to process range queries on arrays. |
2. What Is an Algorithm?
2.1. Definition
An algorithm is a finite set of steps, rules, or instructions arranged in a strict logical sequence to transform input data into the desired output.
Key points:
- Finite: An algorithm must terminate after a limited number of steps.
- Definite: Each step must be clearly defined and unambiguous.
- Executable: Every step must be simple enough for a computer or a human to carry out within a finite amount of time.
An algorithm is independent of any specific programming language. It can be described using:
- Natural language: verbal or written descriptions.
- Flowcharts: diagrams using symbols to represent the processing flow.
- Pseudocode: a code-like description that is easier to read than actual code.
- Programming languages: direct implementation as executable code.
An algorithm is the “recipe” for solving a problem, while a computer program is the “dish” cooked based on that recipe. A good recipe helps you cook faster, use fewer ingredients, and adapt it more easily.
2.2. Characteristics of Algorithms
An algorithm is not merely a sequence of steps; it must also satisfy certain criteria to be considered valid and effective. Below are four core characteristics:
1. Correctness
An algorithm is considered correct if it always produces the correct result for every valid input.
- This means that if a problem requires finding the largest number in a list, the algorithm must always return the correct maximum value, regardless of the number of elements in the list.
- Correctness is often proven through logical reasoning or mathematical proofs, such as mathematical induction.
- An incorrect algorithm may run quickly, but if the result is wrong, it has no practical value.
Example: Binary search is correct because it always finds the position of an element (if it exists) in a sorted array.
2. Finiteness
An algorithm must terminate after a finite number of steps and must not run indefinitely.
- If an algorithm never terminates, it cannot be used in practice.
- Finiteness ensures that users receive results within a reasonable amount of time.
In programming, forgetting a termination condition in a loop is a common mistake that causes an algorithm to lose its finiteness. - Example: An algorithm that computes the sum of numbers from 1 to n finishes after n steps and is therefore finite.
3. Definiteness
Each step of an algorithm must be clearly and unambiguously defined so that anyone (or any computer) executing it will obtain the same result.
- Vague instructions such as “do what seems reasonable” or “choose an appropriate element” must be avoided.
- Definiteness allows an algorithm to be implemented accurately in source code.
- This is a crucial factor in ensuring the feasibility of implementing an algorithm on a computer.
Example: “If the middle element is greater than the target value, search the left half” is a clear step in binary search.
4. Input/Output
An algorithm must have well-defined inputs and outputs.
- The input is the initial data that the algorithm processes.
- The output is the final result after executing all steps.
An algorithm without output does not solve a problem; without input, there is nothing to process. - Example: A sorting algorithm takes an unsorted list as input and produces a list sorted in ascending order as output.
Conclusion
The four characteristics above form the foundation for evaluating whether an algorithm is valid. In practice, a good algorithm is not only correct and finite, but also clear enough to be easily implemented, and has well-defined inputs and outputs to serve a specific purpose. Understanding these characteristics helps programmers design and choose algorithms that are appropriate for each problem.
2.3. Evaluating Algorithm Performance
The performance of an algorithm reflects how fast it runs and how efficiently it uses resources when solving a problem. There are two main criteria for evaluation:
1. Time Complexity
This measures the number of steps an algorithm requires to complete its task, depending on the input size n.
It is expressed using Big-O notation: Big-O helps describe the growth rate of running time as the input size increases.
| Notation | Description | Example |
|---|---|---|
| O(1) | Constant time | Accessing an element in an array |
| O(log n) | Grows slowly | Binary search |
| O(n) | Linear growth | Traversing an array |
| O(n log n) | Faster than linear growth | Merge Sort, Quick Sort |
| O(n²) | Quadratic growth | Selection sort, bubble sort |
| O(2ⁿ), O(n!) | Extremely rapid growth | Solving combinatorial problems, complex recursion |
Meaning:
- Algorithms with lower complexity handle large datasets more efficiently.
- In practice, we prioritize choosing algorithms with the best possible complexity while still ensuring correctness.
2. Space Complexity
This measures the amount of memory an algorithm requires during execution.
Some algorithms need additional arrays, lookup tables, or stacks to perform their tasks.
Space complexity is also expressed using Big-O notation, such as O(1), O(n), O(n²), etc.
Examples:
- An algorithm that finds the maximum element in an array may require only O(1) extra memory.
- Dynamic programming often requires O(n) or O(n²) space to store intermediate results.
3. Time–Space Trade-off
In many cases, there is a balance between time and memory usage:
- Using extra memory to increase speed (for example, storing results to avoid recomputation).
- Reducing memory usage while accepting longer execution time.
Example:
- A dynamic programming solution to the Fibonacci problem is faster than pure recursion, but it uses additional memory to store results.
4. Empirical vs. Theoretical Analysis
- Theoretical analysis: Uses Big-O notation to evaluate performance in the worst case, average case, and best case.
- Empirical analysis: Runs the algorithm on real data to measure actual time and memory consumption.
Conclusion
Evaluating performance helps us choose algorithms that are suitable for the problem and the execution environment. An algorithm that is correct but slow or consumes too much memory will not be effective in practice. Therefore, complexity analysis is an indispensable step in the design and selection of algorithms.
2.4. Classification of Common Algorithm Categories
| Algorithm Type | Short Description | Examples |
|---|---|---|
| Searching | Finding an element in a dataset | Linear search, binary search |
| Sorting | Arranging data in a specific order | Quick Sort, Merge Sort, Bubble Sort |
| Recursion | Calling itself to solve subproblems | Factorial calculation, tree traversal |
| Greedy | Choosing the locally optimal option at each step | Dijkstra, Kruskal |
| Dynamic Programming | Storing intermediate results to optimize time | Knapsack, Fibonacci |
| Backtracking | Trying all possibilities and backtracking upon failure | Sudoku, N-Queens |
| Divide and Conquer | Dividing a large problem into smaller ones, solving them, then combining the results | Merge Sort, Quick Sort, Binary Search |
| Graph Algorithms | Solving problems on graph structures | BFS, DFS, Dijkstra, Prim |
| Heuristic / Metaheuristic Algorithms | Approximate methods for complex optimization problems | Genetic Algorithm, Simulated Annealing |
| Cryptographic / Security Algorithms | Used in information security | RSA, AES, SHA |
| Machine Learning Algorithms | Learning from data to predict or classify | Linear Regression, Decision Tree |
3. The Relationship Between Data Structures and Algorithms
The relationship between data structures and algorithms is one of the core foundations of computer science. They do not exist independently but are always closely connected. To clarify this relationship, we can analyze it from the following aspects:
3.1. Conceptual Connection
- Data Structure (DS): The way data is organized, arranged, and stored in memory (RAM, disk) so that it can be accessed and modified efficiently.
- Algorithm: A sequence of ordered processing steps to solve a problem on that data.
📌 Key point: An algorithm is merely the “recipe” for processing, while a data structure is the “ingredients” and the “method of storing the ingredients.” Well-organized data makes the recipe easier and faster to execute.
3.2. Mutual Dependence
- Algorithms need data structures: You cannot run an efficient algorithm if the data is not organized properly.
- Data structures need algorithms: A data structure is only useful if there are algorithms to insert, delete, search, and traverse it efficiently.
⟹ Data structures and algorithms always go hand in hand; changing one affects the other.
3.3. Impact on Performance
Data structures directly affect:
- Algorithm running time (Time Complexity).
- Memory consumption (Space Complexity).
- The simplicity or complexity of implementation.
Examples:
| Problem | Chosen Data Structure | Algorithm | Complexity |
|---|---|---|---|
| Searching in a large sorted dataset | Static array | Binary Search | O(log n) |
| Searching with a unique key | Hash table | Hash lookup | Average O(1) |
| Managing a priority queue | Heap | Heap push/pop | O(log n) |
| Shortest path finding | Graph (Adjacency List) | Dijkstra | O((V + E) log V) |
3.4. Mutual Influence
Data Structure → Algorithm
- If data is stored in a sorted array, binary search can be used.
- If data is stored in a linked list, binary search is not feasible because middle elements cannot be accessed in O(1).
Algorithm → Data Structure
- If Dijkstra’s algorithm is required, a priority queue (heap) is chosen to reduce the time needed to extract the minimum vertex.
- If a regular array is used to find the minimum element each time, the time complexity increases from O(log n) to O(n).
Conclusion:
Algorithms cannot be separated from data structures, because the way data is stored determines how it can be processed and at what speed.
When designing a program, a skilled programmer will first choose appropriate data structures, then select or design suitable algorithms to optimize both time and memory.
4. Benefits of Learning Data Structures and Algorithms
4.1. Solving Problems Faster
When faced with a problem, you will know how to store data and how to process it to obtain results as efficiently as possible.
Examples:
- Searching for a username: If stored in a hash table, lookup is O(1) instead of O(n).
- Task scheduling: Using a priority queue (heap) allows you to quickly retrieve the highest-priority task.
👉 Learning data structures helps you avoid “brute-force coding” (trying all possibilities) and instead find smarter approaches.
4.2. Writing Optimized, Resource-Efficient Code
- Time optimization: Code runs faster and reduces latency.
- Memory optimization: Avoids wasting RAM or storage.
Examples:
- Processing gigabyte-scale log files: Using streaming algorithms so the entire file does not need to be loaded into RAM.
- Building a chat system: Using a circular buffer instead of a regular array to avoid constant data shifting.
👉 This is especially important in mobile applications, games, or embedded systems where resources are limited.
4.3. Passing Programming Interviews More Easily
Major technology companies such as Google, Meta, Amazon, and Microsoft place strong emphasis on data structure skills.
Reasons:
- DSA is a measure of logical thinking and problem-solving ability.
- It is independent of programming languages, making evaluations fairer.
In interviews, you may encounter problems such as:
- Finding the shortest path (Graph + BFS/DFS/Dijkstra).
- Finding a pair of numbers with a given sum (Hash Map).
- Sorting data (Merge Sort, Quick Sort).
👉 Mastering data structures helps you avoid “freezing up” when facing unfamiliar problems.
4.4. Gaining a Deeper Understanding of How Computers Work
When learning data structures, you will:
- Understand how data is stored in RAM, cache, and disk.
- Grasp pointer mechanics, memory access, and complexity.
Examples:
- Why is traversing a contiguous array faster than a linked list? → Because CPU cache works more efficiently when data is stored close together.
- Why does binary search require sorted data? → Because it relies on eliminating half of the data at each step.
👉 This helps you write code that is not only correct but also “hardware-friendly.”
Conclusion
Learning data structures is not just about “passing a course” or “passing interviews”; it is a core skill that helps you:
- Solve problems faster.
- Write cleaner and more efficient code.
- Feel confident when working on real-world projects.
- Understand what is happening “inside” the computer.
5. Final Conclusion
Data structures and algorithms are the foundation of programming, like the “backbone” and the “brain” of all software. A good programmer not only knows how to write code that works correctly, but also knows how to choose appropriate data structures and apply optimized algorithms to save processing time and system resources.
Mastering DSA not only helps you solve problems faster and write cleaner, more efficient code, but also opens the door to passing challenging programming interviews at leading technology companies.
Remember: Data structures and algorithms are tools—the real weapon is problem-solving thinking.
Suggestions
Some platforms for learning Data Structures & Algorithms:
- GeeksforGeeks – A massive collection of DSA materials and exercises, from basic to advanced.
- LeetCode – Algorithm practice, extremely useful for interviews.
- HackerRank – Includes DSA sections with theoretical explanations.
- Codeforces – Competitive programming platform to sharpen skills.
- Visualgo – Visual simulations of how data structures and algorithms work.
6. References
[1] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to Algorithms, 3rd ed. Cambridge, MA, USA: MIT Press, 2009.
[2] R. Sedgewick and K. Wayne, Algorithms, 4th ed. Boston, MA, USA: Addison-Wesley, 2011.
[3] S. S. Skiena, The Algorithm Design Manual, 2nd ed. London, UK: Springer, 2008.
[4] A. Bhargava, Grokking Algorithms: An Illustrated Guide for Programmers and Other Curious People. Shelter Island, NY, USA: Manning Publications, 2016.