Trong thế giới lập trình, cấu trúc dữ liệu (Data Structures) và giải thuật (Algorithms) giống như xương sống và bộ não của phần mềm.
- Cấu trúc dữ liệu giúp bạn tổ chức và lưu trữ dữ liệu một cách khoa học.
- Giải thuật giúp bạn xử lý dữ liệu một cách nhanh chóng và chính xác.
Một lập trình viên giỏi không chỉ biết viết chương trình chạy được, mà còn biết tối ưu hóa thời gian và bộ nhớ, nhờ vào việc chọn cấu trúc dữ liệu và giải thuật phù hợp. Trong bài viết này hãy cùng mình tìm hiểu về cấu trúc dữ liệu và giải thuật: từ khái niệm cơ bản, các loại phổ biến, cho đến cách chúng phối hợp với nhau để tạo nên những chương trình vừa nhanh vừa “tiết kiệm tài nguyên”.

1. Cấu trúc dữ liệu là gì?
1.1. Định nghĩa
Cấu trúc dữ liệu (Data Structure) là cách sắp xếp, tổ chức và lưu trữ dữ liệu trong máy tính sao cho ta có thể truy cập và xử lý chúng một cách hiệu quả.
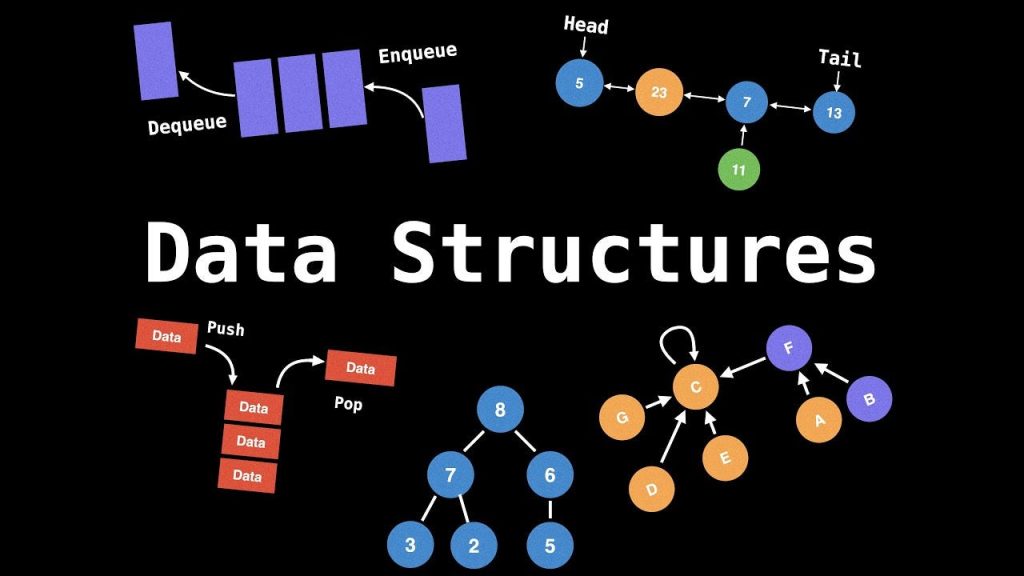
Nói một cách hình tượng:
- Nếu dữ liệu là đống sách vở, tài liệu, file…
- Thì cấu trúc dữ liệu chính là cách bạn xếp chúng trên kệ, phân loại theo chủ đề, đánh số, hoặc bỏ vào hộp để sau này tìm lại nhanh nhất.
Trong khoa học máy tính, việc “hiệu quả” ở đây được đo bằng:
- Thời gian: Mất bao lâu để tìm, thêm, xóa, hay cập nhật dữ liệu? (tính theo độ phức tạp Big-O: O(1), O(log n), O(n), …)
- Bộ nhớ: Mất bao nhiêu dung lượng để lưu trữ? Có lãng phí không?
- Tính linh hoạt: Có dễ mở rộng hoặc thay đổi khi yêu cầu bài toán thay đổi?
Điểm quan trọng: Cùng một dữ liệu, nhưng cách tổ chức khác nhau có thể khiến chương trình chạy nhanh lúc bạn tan làm hoặc chậm như cách bạn chờ crush trả lời tin nhắn của bạn vậy.
Ví dụ: muốn tìm số điện thoại của một người
- Nếu bạn để số điện thoại trong một tờ giấy dài 10.000 dòng và đọc từ đầu đến cuối → mất O(n) thời gian.
- Nếu bạn để nó trong danh bạ đã sắp xếp + dùng tìm kiếm nhị phân → chỉ mất O(log n).
- Nếu bạn để nó trong bảng băm → trung bình O(1) là tìm ra ngay.
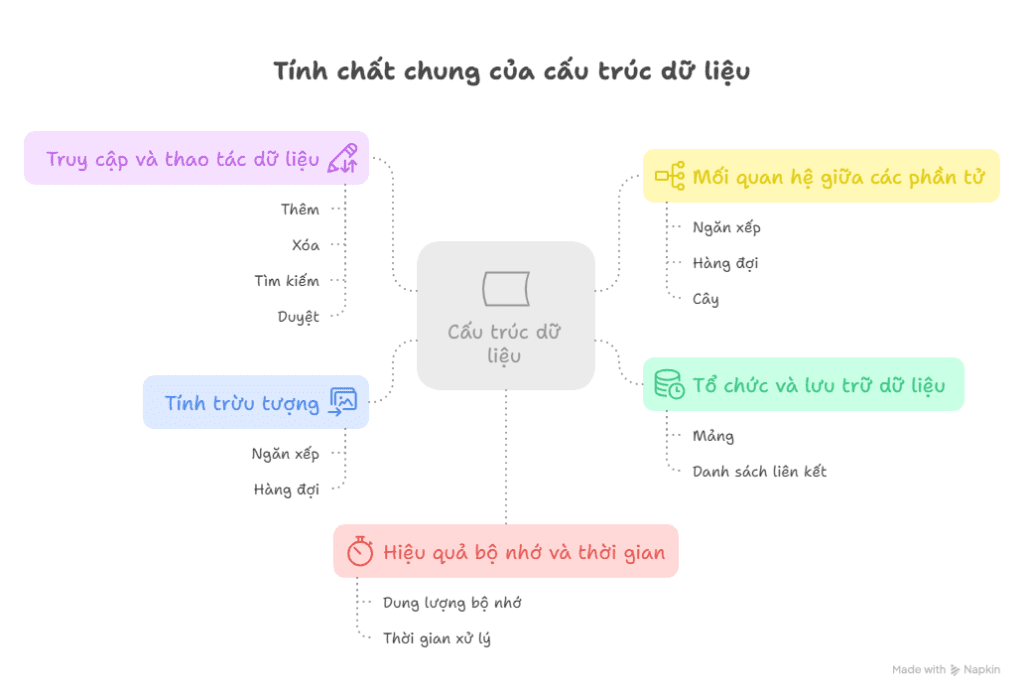
1.2. Tính chất chung của cấu trúc dữ liệu
1. Tổ chức và lưu trữ dữ liệu
- Mỗi cấu trúc dữ liệu đều xác định cách dữ liệu được sắp xếp trong bộ nhớ (liên tiếp hoặc rời rạc).
- Ví dụ:
- Mảng → lưu trữ liên tiếp.
- Danh sách liên kết → lưu trữ rời rạc, kết nối bằng con trỏ.
2. Truy cập và thao tác dữ liệu
- Mỗi loại cấu trúc dữ liệu sẽ hỗ trợ các phép thao tác cơ bản như:
- Thêm (Insert)
- Xóa (Delete)
- Tìm kiếm (Search)
- Duyệt (Traverse)
- Tùy vào cấu trúc mà tốc độ thực hiện khác nhau (O(1), O(log n), O(n)…).
3. Mối quan hệ giữa các phần tử
- Các phần tử có mối liên kết logic (thứ tự, phân cấp, quan hệ cha-con…).
- Ví dụ:
- Ngăn xếp (Stack) → quan hệ LIFO.
- Hàng đợi (Queue) → quan hệ FIFO.
- Cây (Tree) → quan hệ phân cấp.
4. Tính trừu tượng (Abstract)
- Cấu trúc dữ liệu thường được định nghĩa qua các thao tác chứ không quan tâm đến cách cài đặt cụ thể (Abstract Data Type – ADT).
- Ví dụ: “Ngăn xếp” chỉ yêu cầu có
push,pop…; còn cài bằng mảng hay danh sách liên kết thì tùy.
5. Hiệu quả bộ nhớ và thời gian
- Mỗi cấu trúc dữ liệu có ưu và nhược điểm riêng về:
- Dung lượng bộ nhớ.
- Thời gian xử lý thao tác.
- Việc chọn cấu trúc dữ liệu ảnh hưởng trực tiếp đến hiệu năng của chương trình.
1.3. Vai trò của cấu trúc dữ liệu
Cấu trúc dữ liệu đóng vai trò nền tảng trong lập trình và khoa học máy tính, cụ thể:
- Tối ưu hiệu suất chương trình
- Chọn đúng cấu trúc dữ liệu có thể giảm thời gian chạy từ hàng giờ xuống vài giây.
- Tiết kiệm bộ nhớ
- Tổ chức hợp lý giúp hạn chế lãng phí dung lượng, đặc biệt với dữ liệu lớn.
- Dễ bảo trì và mở rộng
- Mã nguồn gọn gàng, rõ ràng hơn khi dữ liệu được quản lý khoa học.
- Giải quyết bài toán phức tạp
- Các thuật toán nâng cao (như tìm đường đi ngắn nhất, lập lịch, phân tích dữ liệu) phụ thuộc mạnh vào cấu trúc dữ liệu phù hợp.
- Nền tảng cho việc học giải thuật
- Nhiều giải thuật chỉ hiệu quả nếu đi kèm cấu trúc dữ liệu đúng loại (ví dụ: Dijkstra cần hàng đợi ưu tiên)
1.4. Các loại cấu trúc dữ liệu phổ biến
Cấu trúc dữ liệu tuyến tính (Linear Data Structures)
| Loại | Mô tả |
|---|---|
| Mảng (Array) | Lưu trữ các phần tử liên tiếp trong bộ nhớ. Truy cập nhanh nhưng kích thước cố định. |
| Danh sách liên kết (Linked List) | Các phần tử liên kết với nhau qua con trỏ. Linh hoạt về kích thước. |
| Ngăn xếp (Stack) | Cấu trúc LIFO (Last In First Out). |
| Hàng đợi (Queue) | Cấu trúc FIFO (First In First Out). |
Cấu trúc dữ liệu phi tuyến tính (Non-linear Data Structures)
| Loại | Mô tả |
|---|---|
| Cây (Tree) | Mỗi nút có thể có nhiều nút con. Dùng để biểu diễn phân cấp. |
| Đồ thị (Graph) | Gồm các đỉnh và cạnh, biểu diễn mối quan hệ giữa các đối tượng. |
Cấu trúc dữ liệu trừu tượng (Abstract Data Types – ADT)
| Loại | Mô tả |
|---|---|
| Danh sách (List) | Tập hợp các phần tử có thứ tự. |
| Tập hợp (Set) | Tập hợp không có phần tử trùng lặp. |
| Bảng băm (Hash Table) | Lưu trữ dữ liệu theo cặp khóa–giá trị. Truy cập nhanh. |
| Ưu tiên hàng đợi (Priority Queue) | Hàng đợi mà phần tử có độ ưu tiên cao được xử lý trước. |
Cấu trúc dữ liệu đặc biệt
| Loại | Mô tả |
|---|---|
| Heap | Cây nhị phân đặc biệt dùng để tìm giá trị lớn nhất/nhỏ nhất nhanh. |
| Trie (Cây tiền tố) | Cây dùng để lưu trữ chuỗi, đặc biệt là từ điển. |
| Segment Tree / Fenwick Tree | Cấu trúc nâng cao dùng để xử lý truy vấn trên mảng. |
2. Giải thuật là gì?
2.1. Định nghĩa
Giải thuật là một tập hợp hữu hạn các bước, quy tắc hoặc chỉ dẫn được sắp xếp theo một trình tự logic chặt chẽ, nhằm biến dữ liệu đầu vào thành kết quả đầu ra mong muốn.
Điểm quan trọng:
- Hữu hạn: giải thuật phải kết thúc sau một số bước nhất định.
- Xác định: mỗi bước phải được mô tả rõ ràng, không gây mơ hồ.
- Có thể thực thi: mọi bước phải đủ đơn giản để máy tính hoặc con người thực hiện được trong thời gian hữu hạn.
Giải thuật không phụ thuộc vào ngôn ngữ lập trình cụ thể. Nó có thể được mô tả bằng:
- Ngôn ngữ tự nhiên: mô tả bằng lời văn.
- Lưu đồ (flowchart): dùng ký hiệu để thể hiện luồng xử lý.
- Giả mã (pseudocode): mô tả cú pháp gần giống code nhưng dễ đọc hơn.
- Ngôn ngữ lập trình: triển khai trực tiếp thành code chạy được.
Giải thuật là “công thức” giải bài toán, còn chương trình máy tính là “món ăn” được nấu dựa trên công thức đó. Một công thức tốt sẽ giúp bạn nấu nhanh, tốn ít nguyên liệu và dễ biến tấu.
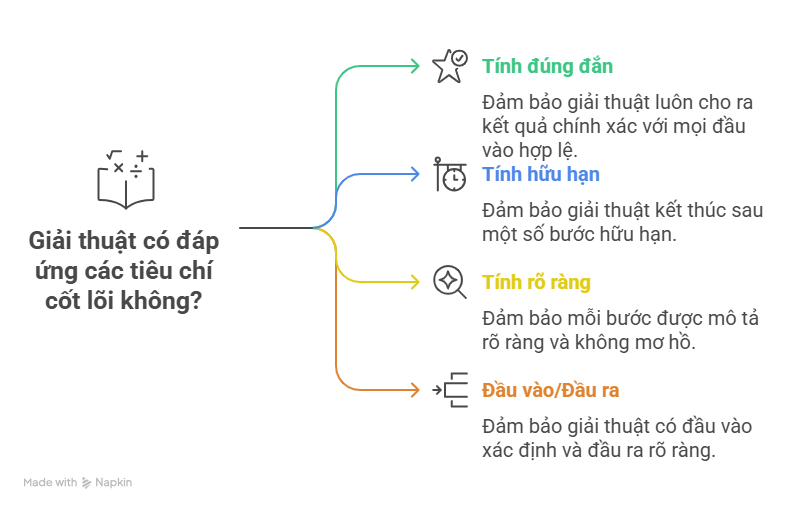
2.2 Đặc điểm của giải thuật
Một giải thuật không chỉ là một chuỗi các bước thực hiện, mà còn phải đáp ứng những tiêu chí nhất định để được xem là hợp lệ và hiệu quả. Dưới đây là bốn đặc điểm cốt lõi:
1. Tính đúng đắn (Correctness)
Giải thuật được gọi là đúng đắn nếu nó luôn cho ra kết quả chính xác với mọi đầu vào hợp lệ.
- Điều này có nghĩa là: nếu bài toán yêu cầu tìm số lớn nhất trong một danh sách, thì giải thuật phải luôn trả về đúng số lớn nhất, bất kể danh sách có bao nhiêu phần tử.
- Tính đúng đắn thường được chứng minh bằng lập luận logic hoặc chứng minh toán học, ví dụ như quy nạp toán học.
- Một giải thuật sai có thể chạy nhanh, nhưng nếu kết quả sai thì không có giá trị thực tiễn.
Ví dụ: Giải thuật tìm kiếm nhị phân là đúng đắn vì nó luôn tìm ra vị trí của phần tử (nếu tồn tại) trong một mảng đã sắp xếp.
2. Tính hữu hạn (Finiteness)
Giải thuật phải kết thúc sau một số bước hữu hạn, không được chạy vô hạn.
- Nếu một giải thuật không bao giờ kết thúc, nó không thể được sử dụng trong thực tế.
- Tính hữu hạn đảm bảo rằng người dùng sẽ nhận được kết quả trong một khoảng thời gian hợp lý.
- Trong lập trình, việc quên điều kiện dừng trong vòng lặp là một lỗi phổ biến khiến giải thuật mất tính hữu hạn.
Ví dụ: Giải thuật tính tổng các số từ 1 đến n sẽ kết thúc sau n bước, nên là hữu hạn.
3. Tính rõ ràng (Definiteness)
Mỗi bước trong giải thuật phải được mô tả rõ ràng, không mơ hồ, để bất kỳ ai (hoặc máy tính) thực hiện cũng cho ra kết quả giống nhau.
- Không được sử dụng các chỉ dẫn mơ hồ như “làm như bạn thấy hợp lý” hay “chọn phần tử phù hợp”.
- Tính rõ ràng giúp giải thuật có thể được hiện thực hóa bằng mã nguồn một cách chính xác.
- Đây là yếu tố quan trọng để đảm bảo tính khả thi khi triển khai giải thuật trên máy tính.
Ví dụ: “Nếu phần tử ở giữa lớn hơn giá trị cần tìm, thì tìm ở nửa bên trái” là một bước rõ ràng trong tìm kiếm nhị phân.
4. Tính đầu vào/đầu ra (Input/Output)
Giải thuật cần có đầu vào xác định và đầu ra rõ ràng.
- Đầu vào là dữ liệu ban đầu mà giải thuật xử lý.
- Đầu ra là kết quả cuối cùng sau khi thực hiện các bước.
- Một giải thuật không có đầu ra thì không giải quyết được bài toán; không có đầu vào thì không có gì để xử lý.
Ví dụ: Giải thuật sắp xếp nhận đầu vào là một danh sách chưa sắp xếp, và đầu ra là danh sách đã được sắp xếp theo thứ tự tăng dần.
Tổng kết
Bốn đặc điểm trên là nền tảng để đánh giá một giải thuật có hợp lệ hay không. Trong thực tế, một giải thuật tốt không chỉ đúng đắn và hữu hạn, mà còn phải rõ ràng để dễ triển khai, và có đầu vào/đầu ra rõ ràng để phục vụ mục tiêu cụ thể. Việc hiểu rõ các đặc điểm này giúp lập trình viên thiết kế và lựa chọn giải thuật phù hợp với từng bài toán.
2.3 Đánh giá hiệu suất giải thuật
Hiệu suất của một giải thuật phản ánh mức độ nhanh và tiết kiệm tài nguyên khi giải quyết một bài toán. Có hai tiêu chí chính để đánh giá:
1. Độ phức tạp thời gian (Time Complexity)
Đây là thước đo số lượng bước thực hiện mà giải thuật cần để hoàn thành công việc, tùy theo kích thước đầu vào n.
Biểu diễn bằng ký hiệu Big-O:
Big-O giúp ta mô tả tốc độ tăng trưởng của thời gian chạy khi đầu vào tăng.
| Ký hiệu | Mô tả | Ví dụ |
|---|---|---|
| O(1) | Thời gian không đổi | Truy cập phần tử trong mảng |
| O(log n) | Tăng chậm | Tìm kiếm nhị phân |
| O(n) | Tăng tuyến tính | Duyệt qua mảng |
| O(n log n) | Tăng nhanh hơn tuyến tính | Merge Sort, Quick Sort |
| O(n²) | Tăng theo bình phương | Sắp xếp chọn, sắp xếp nổi bọt |
| O(2ⁿ), O(n!) | Tăng cực nhanh | Giải bài toán tổ hợp, đệ quy phức tạp |
Ý nghĩa:
- Giải thuật có độ phức tạp thấp sẽ xử lý nhanh hơn khi dữ liệu lớn.
- Trong thực tế, ta ưu tiên chọn giải thuật có độ phức tạp tốt nhất có thể, nhưng vẫn đảm bảo tính đúng đắn.
2. Độ phức tạp không gian (Space Complexity)
Đây là thước đo lượng bộ nhớ mà giải thuật cần sử dụng trong quá trình thực hiện.
- Một số giải thuật cần thêm mảng phụ, bảng lưu trữ, hoặc ngăn xếp để xử lý.
- Độ phức tạp không gian cũng được biểu diễn bằng Big-O, ví dụ: O(1), O(n), O(n²)…
Ví dụ:
- Giải thuật tìm phần tử lớn nhất trong mảng có thể chỉ cần O(1) bộ nhớ.
- Quy hoạch động thường cần O(n) hoặc O(n²) để lưu kết quả trung gian.
3. Trade-off giữa thời gian và không gian
Trong nhiều trường hợp, ta phải cân bằng giữa thời gian và bộ nhớ:
- Dùng thêm bộ nhớ để tăng tốc độ (ví dụ: lưu kết quả để tránh tính lại).
- Giảm dùng bộ nhớ nhưng chấp nhận thời gian chạy lâu hơn.
Ví dụ:
- Giải thuật quy hoạch động giải bài toán Fibonacci nhanh hơn đệ quy thuần, nhưng tốn thêm bộ nhớ để lưu kết quả.
4. Phân tích thực nghiệm vs lý thuyết
- Phân tích lý thuyết: Dựa vào Big-O để đánh giá hiệu suất trong trường hợp xấu nhất, trung bình, tốt nhất.
- Phân tích thực nghiệm: Chạy thử giải thuật với dữ liệu thực tế để đo thời gian và bộ nhớ tiêu thụ.
Tổng kết
Đánh giá hiệu suất giúp ta chọn được giải thuật phù hợp với bài toán và môi trường thực thi. Một giải thuật đúng đắn nhưng chậm hoặc tốn quá nhiều bộ nhớ sẽ không hiệu quả trong thực tế. Vì vậy, việc phân tích độ phức tạp là bước không thể thiếu trong thiết kế và lựa chọn giải thuật.
2.4 Bảng phân loại các nhóm giải thuật phổ biến
| Loại thuật toán | Mô tả ngắn | Ví dụ |
|---|---|---|
| Tìm kiếm (Searching) | Tìm phần tử trong tập dữ liệu | Tìm kiếm tuyến tính, nhị phân |
| Sắp xếp (Sorting) | Sắp xếp dữ liệu theo thứ tự | Quick Sort, Merge Sort, Bubble Sort |
| Đệ quy (Recursion) | Gọi lại chính nó để giải bài toán con | Tính giai thừa, duyệt cây |
| Tham lam (Greedy) | Chọn phương án tối ưu tại mỗi bước | Dijkstra, Kruskal |
| Quy hoạch động (Dynamic Programming) | Lưu kết quả trung gian để tối ưu thời gian | Knapsack, Fibonacci |
| Backtracking | Thử từng khả năng, quay lui khi sai | Sudoku, N-Queens |
| Chia để trị (Divide and Conquer) | Chia bài toán lớn thành bài toán nhỏ, giải từng phần rồi kết hợp | Merge Sort, Quick Sort, Binary Search |
| Thuật toán đồ thị (Graph Algorithms) | Giải bài toán trên cấu trúc đồ thị | BFS, DFS, Dijkstra, Prim |
| Thuật toán heuristic / metaheuristic | Gần đúng, dùng trong bài toán tối ưu phức tạp | Genetic Algorithm, Simulated Annealing |
| Thuật toán mã hóa / bảo mật | Dùng trong lĩnh vực an toàn thông tin | RSA, AES, SHA |
| Thuật toán học máy (Machine Learning) | Học từ dữ liệu để dự đoán hoặc phân loại | Linear Regression, Decision Tree |
3. Mối quan hệ giữa cấu trúc dữ liệu và giải thuật
Mối quan hệ giữa cấu trúc dữ liệu và giải thuật là một trong những nền tảng cốt lõi của khoa học máy tính. Chúng không tồn tại độc lập mà luôn gắn bó chặt chẽ với nhau. Để làm rõ vấn đề này, ta có thể phân tích theo các khía cạnh sau:
3.1 Khái niệm kết nối
- Cấu trúc dữ liệu (DS): Cách bạn tổ chức, sắp xếp và lưu trữ dữ liệu trong bộ nhớ (RAM, đĩa cứng) để có thể truy cập và thay đổi hiệu quả.
- Giải thuật (Algorithm): Tập hợp các bước xử lý có thứ tự để giải quyết bài toán trên dữ liệu đó.
📌 Điểm mấu chốt: Giải thuật chỉ là “bộ công thức” xử lý, còn cấu trúc dữ liệu chính là “nguyên liệu” và “cách bảo quản nguyên liệu”. Nguyên liệu được tổ chức tốt thì công thức sẽ dễ làm và nhanh hơn.
3.2 Tính phụ thuộc lẫn nhau
- Giải thuật cần DS: Bạn không thể chạy một giải thuật hiệu quả nếu dữ liệu không được tổ chức hợp lý.
- DS cần giải thuật: Một DS chỉ hữu ích nếu có các giải thuật để thêm, xóa, tìm kiếm, duyệt nó nhanh chóng.
⟹ DS và Algorithm luôn song hành: thay đổi một bên sẽ tác động đến bên còn lại.
3.3 Tác động đến hiệu suất
Cấu trúc dữ liệu ảnh hưởng trực tiếp đến:
- Thời gian chạy của giải thuật (Time Complexity).
- Bộ nhớ tiêu thụ (Space Complexity).
- Tính đơn giản/phức tạp khi cài đặt.
Ví dụ:
| Bài toán | Cấu trúc dữ liệu chọn | Giải thuật | Độ phức tạp |
|---|---|---|---|
| Tìm kiếm trong tập lớn đã sắp xếp | Mảng tĩnh (Array) | Binary Search | O(log n) |
| Tìm kiếm với khóa duy nhất | Hash Table | Tra cứu theo băm | O(1) trung bình |
| Quản lý hàng đợi ưu tiên | Heap | Heap Push/Pop | O(log n) |
| Tìm đường ngắn nhất | Đồ thị (Adjacency List) | Dijkstra | O((V+E) log V) |
3.4 Tác động qua lại
Data Structure → Algorithm
- Nếu dữ liệu lưu dưới dạng mảng đã sắp xếp, bạn có thể dùng Binary Search.
- Nếu lưu dưới dạng linked list, Binary Search không khả thi vì không thể truy cập phần tử giữa O(1).
Algorithm → Data Structure
- Nếu cần thuật toán Dijkstra, bạn sẽ chọn Priority Queue (Heap) để giảm thời gian lấy đỉnh nhỏ nhất.
- Nếu dùng mảng thường để tìm phần tử nhỏ nhất mỗi lần, thời gian sẽ tăng từ O(log n) thành O(n).
Kết luận:
- Giải thuật không thể tách rời cấu trúc dữ liệu vì dữ liệu lưu trữ thế nào sẽ quyết định cách và tốc độ xử lý.
- Khi thiết kế chương trình, lập trình viên giỏi sẽ chọn cấu trúc dữ liệu trước, sau đó chọn hoặc thiết kế giải thuật phù hợp để tối ưu cả thời gian và bộ nhớ.
4. Lợi ích khi học Cấu trúc dữ liệu và Giải thuật
4.1. Giải quyết vấn đề nhanh hơn
- Khi gặp một bài toán, bạn sẽ biết phải lưu dữ liệu thế nào và xử lý ra sao để ra kết quả nhanh nhất.
- Ví dụ:
- Tìm kiếm tên người dùng: Nếu lưu trong Hash Table, tra cứu O(1) thay vì O(n).
- Lập lịch xử lý công việc: Dùng Priority Queue (Heap) để luôn lấy việc ưu tiên cao nhất nhanh chóng.
- 👉 Học Data Structure giúp bạn tránh “code kiểu brute force” (duyệt hết mọi khả năng) và thay vào đó tìm cách thông minh hơn.
4.2. Viết code tối ưu, tiết kiệm tài nguyên
- Tối ưu thời gian: Code chạy nhanh hơn, giảm độ trễ.
- Tối ưu bộ nhớ: Tránh lãng phí RAM hoặc lưu trữ.
- Ví dụ:
- Xử lý log file hàng GB: dùng Streaming Algorithm để không cần load toàn bộ vào RAM.
- Xây dựng hệ thống chat: dùng Circular Buffer thay vì mảng thường để tránh dịch chuyển dữ liệu liên tục.
- 👉 Điều này rất quan trọng trong ứng dụng di động, game hoặc hệ thống nhúng nơi tài nguyên hạn chế.
4.3. Vượt qua phỏng vấn lập trình dễ dàng hơn
- Các công ty công nghệ lớn như Google, Meta, Amazon, Microsoft rất chú trọng kỹ năng Data Structure.
- Lý do:
- DSA là thước đo khả năng tư duy logic và giải quyết vấn đề.
- Nó độc lập với ngôn ngữ lập trình, nên đánh giá công bằng.
- Trong phỏng vấn, bạn sẽ gặp dạng:
- Tìm đường đi ngắn nhất (Graph + BFS/DFS/Dijkstra).
- Tìm cặp số có tổng bằng X (Hash Map).
- Sắp xếp dữ liệu (Merge Sort, Quick Sort).
- 👉 Nắm vững Data Structure giúp bạn không bị “đứng hình” khi gặp bài lạ.
4.4. Hiểu sâu cách máy tính hoạt động
- Khi học Data Structure, bạn sẽ:
- Hiểu cách dữ liệu lưu trong RAM, Cache, Ổ đĩa.
- Nắm rõ cơ chế con trỏ, truy cập bộ nhớ, độ phức tạp.
- Ví dụ:
- Tại sao mảng liên tiếp lại duyệt nhanh hơn linked list? → vì cache CPU hoạt động tốt hơn khi dữ liệu nằm gần nhau.
- Tại sao tìm kiếm nhị phân cần dữ liệu đã sắp xếp? → vì nó dựa vào việc loại bỏ nửa dữ liệu mỗi bước.
- 👉 Điều này giúp bạn viết code không chỉ đúng mà còn “thân thiện” với phần cứng.
Kết luận
Học Data Structure không chỉ là để “qua môn” hay “qua vòng phỏng vấn”, mà nó là kỹ năng cốt lõi giúp bạn:
- Giải bài toán nhanh hơn.
- Code gọn và hiệu quả hơn.
- Tự tin khi làm dự án thực tế.
- Hiểu rõ “bên trong” máy tính đang làm gì.
5. Kết luận
Cấu trúc dữ liệu và giải thuật chính là nền móng của lập trình, giống như “xương sống” và “bộ não” của mọi phần mềm. Một lập trình viên giỏi không chỉ biết viết code chạy đúng, mà còn biết chọn cấu trúc dữ liệu phù hợp và áp dụng giải thuật tối ưu để tiết kiệm thời gian xử lý và tài nguyên hệ thống.
Việc thành thạo DSA không chỉ giúp bạn giải quyết vấn đề nhanh hơn, viết code gọn gàng và hiệu quả hơn, mà còn mở ra cơ hội vượt qua các kỳ phỏng vấn lập trình khó khăn tại những công ty công nghệ hàng đầu.
Hãy nhớ: Cấu trúc dữ liệu và giải thuật là công cụ — còn tư duy giải quyết vấn đề mới là vũ khí thật sự.
Gợi ý
Một số trang học Cấu trúc dữ liệu & Giải thuật
- GeeksforGeeks – Kho tài liệu và bài tập DSA khổng lồ, từ cơ bản đến nâng cao.
- LeetCode – Luyện tập giải thuật, cực hữu ích cho phỏng vấn.
- HackerRank – Có phần DSA kèm giải thích lý thuyết.
- Codeforces – Trang thi lập trình cạnh tranh, giúp nâng kỹ năng.
- Visualgo – Mô phỏng trực quan cách hoạt động của các cấu trúc dữ liệu và thuật toán.
6. Tài liệu tham khảo
- Introduction to Algorithms – Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
- Algorithms (4th Edition) – Robert Sedgewick, Kevin Wayne
- The Algorithm Design Manual – Steven S. Skiena
- Grokking Algorithms – Aditya Bhargava



